FFT 快速傅里叶变换

前置知识

复数

多项式

形如

F(x)=\sum_{i=0}^n a_i x^i

的式子。其中 $n$ 为非负整数。我们只需知道所有 $a_i$ ，就可以确定一个多项式。这就是多项式的系数表示法。

为了方便运算，我们引入多项式的点值表示法。

对于一个 $n$ 次多项式 $F(x)$ ，我们可以用 $n+1$ 个互不相同的点 $\{(x_0,F(x_0)),(x_1,F(x_1)),\cdots,(x_{n+1},F(x_{n+1}))\}$ 来确定这个多项式。我们下文称这个集合为 $S_{F(x)}$ 。

系数表示法转为点值表示法的过程叫做 DFT，反之叫 IDFT。

卷积

$H(x)=F(x)\times G(x)$ 表示 $H(x)$ 为 $F(x)$ 和 $G(x)$ 的卷积。

刚才的多项式乘法求得的式子并不是标准的多项式形式。我们设 $H(x)=F(x)\times G(x)=\sum_{k=0}^{n+m}c_kx^k$ 。则每项的系数 $c_k=\sum_{i+j=k}a_ib_j$ ，变为更容易计算的形式

c_k=\sum_{i=\max(0,k-m)}^{\min(n,k)}a_ib_{k-i}

若使用点值表示法，设

S_{F(x)}=\{(x_i,y_i)\}

S_{G(x)}=\{(x_i,y'_i)\}

则有

S_{H(x)}=\{(x_i,y_iy'_i)\}

单位根

根据代数基本定理^[1]， $x^n=1$ 有 $n$ 个根，这 $n$ 个根都称为单位根。记作 $\{\omega_n^k\mid k=0,1,\cdots,n-1\}$ ，其中， $\omega_n^0=1$ 。在复平面上，它们刚好将单位圆 $n$ 等分。一般说的单位根 $\omega_n$ ，指从 $(1,0)$ 开始逆时针方向上的第一个根。

一些下面会用到的小式子：

对于偶数次单位根，有 $\omega_n^i=-\omega_n^{i+\frac{n}{2}}$ （其实就是在复平面上关于原点中心对称）。
$\omega_{2n}^{2k}=\omega_n^k$
$(\omega_n^k)^2=\omega_n^{2k}$

FFT

显然，朴素算法求解 $F(x) * G(x)$ 的时间复杂度为 $O(nm)$ ，而 FFT 可以让我们在 $O(n\log n)$ 的时间复杂度内计算两个 $n$ 次多项式的乘法。基本思想是分治。

我们只需对 $F(x)$ 和 $G(x)$ 进行 DFT，计算 $S_{H(x)}=S_{F(x)}*S_{G(x)}$ ，最后再对 $S_{H(x)}$ IDFT 即得 $H(x)$ 。

接下来说 DFT 的过程。

对于 $F(x)$ ，将其划分为奇次与偶次两部分。

F(x)=\sum_{i=0}^{\frac{n}{2}}a_{2i}x^{2i}+\sum_{i=0}^{\frac{n}{2}}a_{2i+1}x^{2i+1}

将右半部分提出一个 $x$

F(x)=\sum_{i=0}^{\frac{n}{2}}a_{2i}x^{2i}+x\sum_{i=0}^{\frac{n}{2}}a_{2i+1}x^{2i}

将前后两部分用新的多项式表示

F_1(x)=\sum_{i=0}^{\frac{n}{2}}a_{2i}x^{i}

F_2(x)=\sum_{i=0}^{\frac{n}{2}}a_{2i+1}x^{i}

F(x)=F_1(x^2)+xF_2(x^2)

这时我们代入 $\omega_n^k$ ，可得

\begin{aligned} F(\omega_n^k)&=F_1((\omega_n^k)^2)+\omega_n^kF_2((\omega_n^k)^2)\\ &=F_1(\omega_n^{2k})+\omega_n^kF_2(\omega_n^{2k})\\ &=F_1(\omega_\frac{n}{2}^k)+\omega_n^kF_2(\omega_\frac{n}{2}^k) \end{aligned}

同理，代入 $\omega_n^{k+\frac{n}{2}}=-\omega_n^k$ ，得

F(\omega_n^{k+\frac{n}{2}})=F_1(\omega_\frac{n}{2}^k)-\omega_n^kF_2(\omega_\frac{n}{2}^k)

所以，我们可以根据 $F_1(\omega_\frac{n}{2}^k)$ 和 $F_2(\omega_\frac{n}{2}^k)$ 求出 $F(\omega_n^k)$ 和 $F(\omega_n^{k+\frac{n}{2}})$ 。这种做法只能处理长度为 $2$ 的正整次幂的多项式，所以我们要把高次系数补为 $0$ 。

接下来是 IDFT。它的操作与 DFT 极像，就是将 $\omega_n^k$ 变为 $\omega_n^{-k}$ ，并在最后乘 $\dfrac{1}{n}$ 。

现实计算中，递归处理效率较低，我们使用位逆序置换优化和蝶形运算优化，直接将值排列为特定的顺序，避免了递归和额外的临时数组。

位逆序置换与蝶形运算

我们要想避免递归，就要将需要一起计算的部分放在一起。

我们以 $7$ 次多项式为例，有 $8$ 个 $a_i$ ，具体划分方式如图

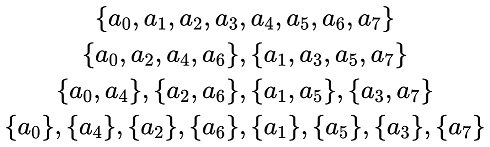
规律很难注意到，我直接说了，就是将每个下标的二进制反转，以反转后的数为新下标。例如， $3$ 的二进制是 $011$ ，反转后为 $110$ ，即 $6$ ，从图上来看， $a_3$ 确实到了原 $a_6$ 的位置。

位逆序置换后，我们可以直接计算 $F_1(x)$ 和 $F_2(x)$ 而无需临时数组，因为计算要用到的数与计算完成后的数应当被存在相同的下标内，直接覆盖原数就行了。具体地，计算 $F(\omega_n^k)$ 和 $F(\omega_n^{k+\frac{n}{2}})$ 时 $F_1(\omega_\frac{n}{2}^k)$ 的值在下标 $k$ ， $F_2(\omega_\frac{n}{2}^k)$ 的值在下标 $k+\dfrac{n}{2}$ 。

#include<iostream>
#include<cmath>
#include<vector>
using namespace std;
constexpr int N=1<<22;//注意这里 n 需要开到第一个大于 n+m 的 2 的整次幂
const double PI=4*atan(1);//这个 π 的精确度非常高
struct Complex{
    double real,imag;
    friend Complex operator+(const Complex &x,const Complex &y){
        return {x.real+y.real,x.imag+y.imag};
    }
    friend Complex operator-(const Complex &x,const Complex &y){
        return {x.real-y.real,x.imag-y.imag};
    }
    friend Complex operator*(const Complex &x,const Complex &y){
        return {x.real*y.real-x.imag*y.imag,x.real*y.imag+y.real*x.imag};
    }
};
void DFT(vector<Complex> &f,int n,int rev){
    for(int i=0,j=0;i<n;i++){
        if(i<j) swap(f[i],f[j]);
        for(int k=n>>1;(j^=k)<k;k>>=1);
    }
    for(int k=2;k<=n;k<<=1){
        double arg=2*PI*rev/k;
        Complex wn={cos(arg),sin(arg)};
        for(int i=0;i<n;i+=k){
            Complex w={1,0};
            for(int j=0;j<k/2;j++){
                Complex f1=f[i+j];
                Complex f2=f[i+j+k/2];
                f[i+j]=f1+w*f2;
                f[i+j+k/2]=f1-w*f2;
                w=w*wn;
            }
        }
    }
    if(rev==-1)
        for(int i=0;i<n;i++)
            f[i]={f[i].real/n,f[i].imag/n};
}
int n,m,len;
vector<Complex> a,b,c;
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=0,x;i<=n;i++){
        cin>>x;
        a.push_back({double(x),0});
    }
    for(int i=0,x;i<=m;i++){
        cin>>x;
        b.push_back({double(x),0});
    }
    len=1;while(len<=n+m) len<<=1;
    a.resize(len),b.resize(len),c.resize(len);
    DFT(a,len,1);
    DFT(b,len,1);
    for(int i=0;i<len;i++)
        c[i]=a[i]*b[i];
    DFT(c,len,-1);
    for(int i=0;i<=n+m;i++)
        cout<<int(round(c[i].real))<<' ';
    return 0;
}